环形链表

两道环形链表OJ题

环形链表相关问题

环形链表I

此问题的总结来源于两道环形链表的OJ题：环形链表I、环形链表II

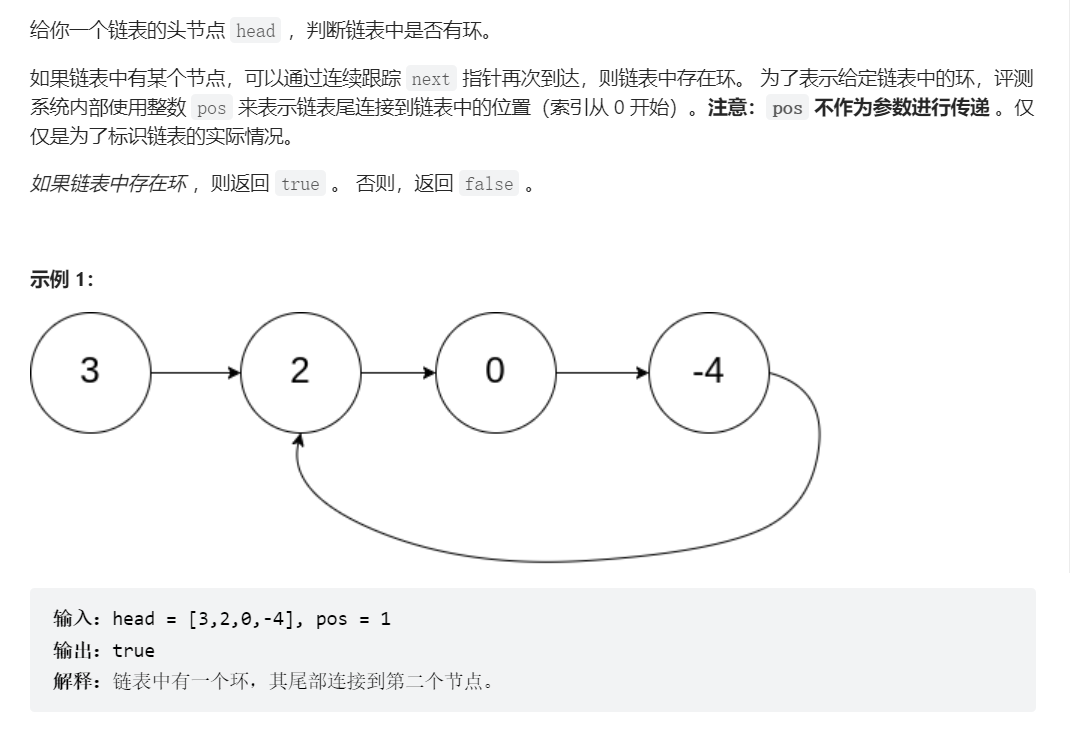
先来看看环形链表I ，题目的是这样的：

按照题目的表述，我们知道如果一个链表不含环，那我通过遍历链表总能找到尾结点。但如果含环，那遍历这个链表就是死循环。我看到这题，可以说是毫无思路，因为我除了遍历也想不到其他的法子。

我了解到“快慢指针”可以很完美的解决这道题。它是这么想的：

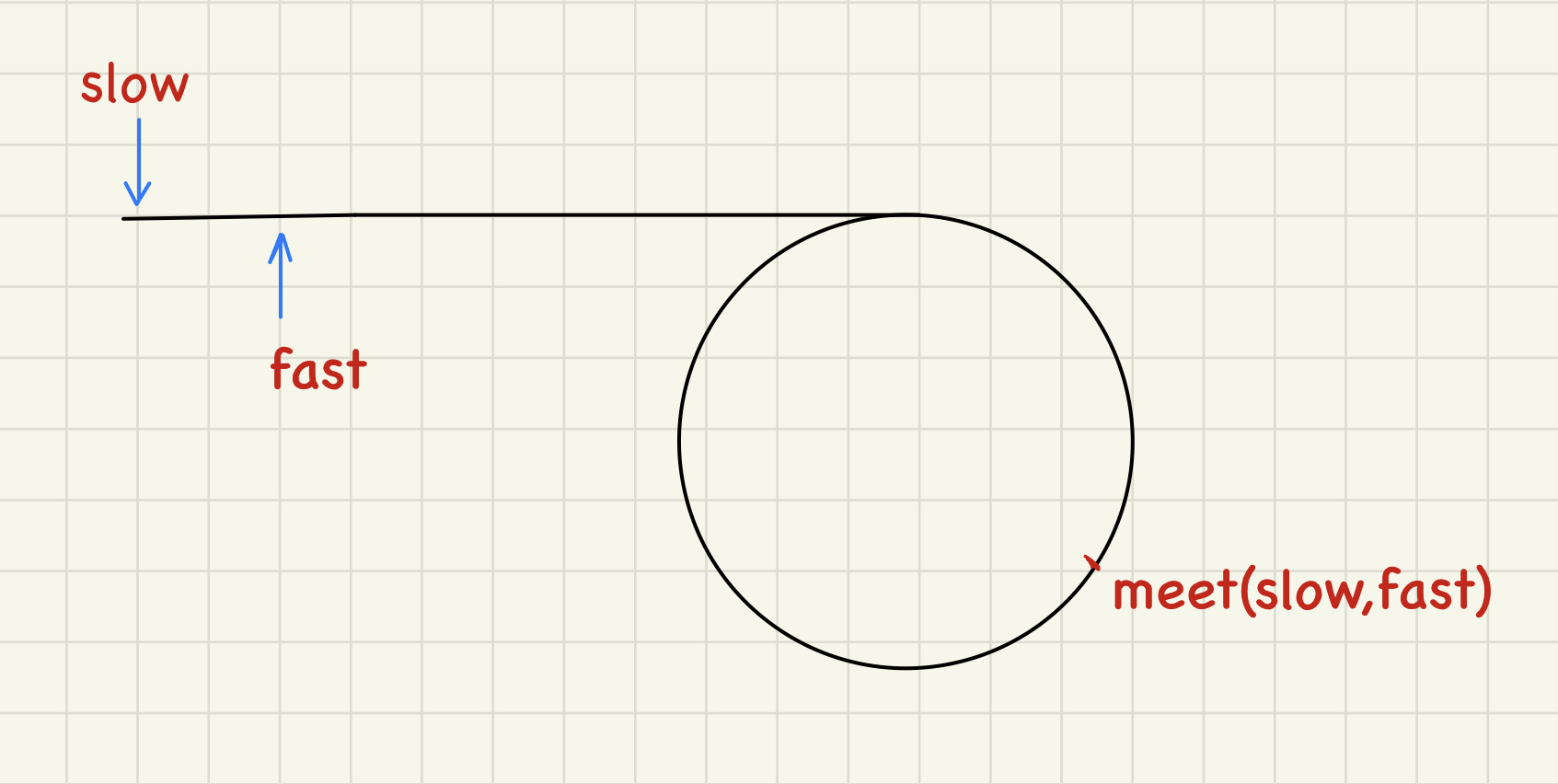
定义两个指针：$slow$和$fast$，让$slow$每次后移一个节点，$fast$每次后移两个结点，如果这个单链表中存在换，当$fast$和$slow$都进环以后，$fast$一定可以追上$slow$。抽象成一个数学问题就是，一个跑的慢的人和一个跑的快的人，从不同起点出发，在环形跑道内跑步，在以后的某一个时刻，跑的快的人一定可以追上跑的慢的人。这是一个很典型的“追击问题”。

​ 示意图

如果fast最后指向了空，那就说明这个链表中是不存在环的。 如果能想明白这个逻辑，那这道题的实现是非常简单的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

bool hasCycle(struct ListNode *head) {
    struct ListNode *fast = head;
    struct ListNode *slow = head;
    while(fast != NULL && fast->next != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(fast == slow)
        {
            return true;
        }
    }
    return false;
}

做完这道题，不妨思考思考这几个问题：

• $fast$一定可以追上$slow$吗？即$fast = slow$；有没有可能它们永远不会相遇？
• $low$一次走1步，$fast$一次走3步，行不行？4步呢？5步呢？

简单想一想第一个问题，直观感觉上如果$fast$一次不走2步，可能fast快碰到$slow$的时候会直接跳过$slow$，那这样$fast$可能不会与$slow$相遇。下面我们需要推导证明这一结论。

我以$fast$一次走3步为例，简单讨论了$slow$与$fast$会不会相遇的问题。当$fast$一次走$4$步时，推导过程类似。此时$N$要满足$N$为3的倍数，或者$C$满足$C-1$、$C-2$均为$3$的倍数时，才会相遇。

由此，总结出一般规律：

环形链表II

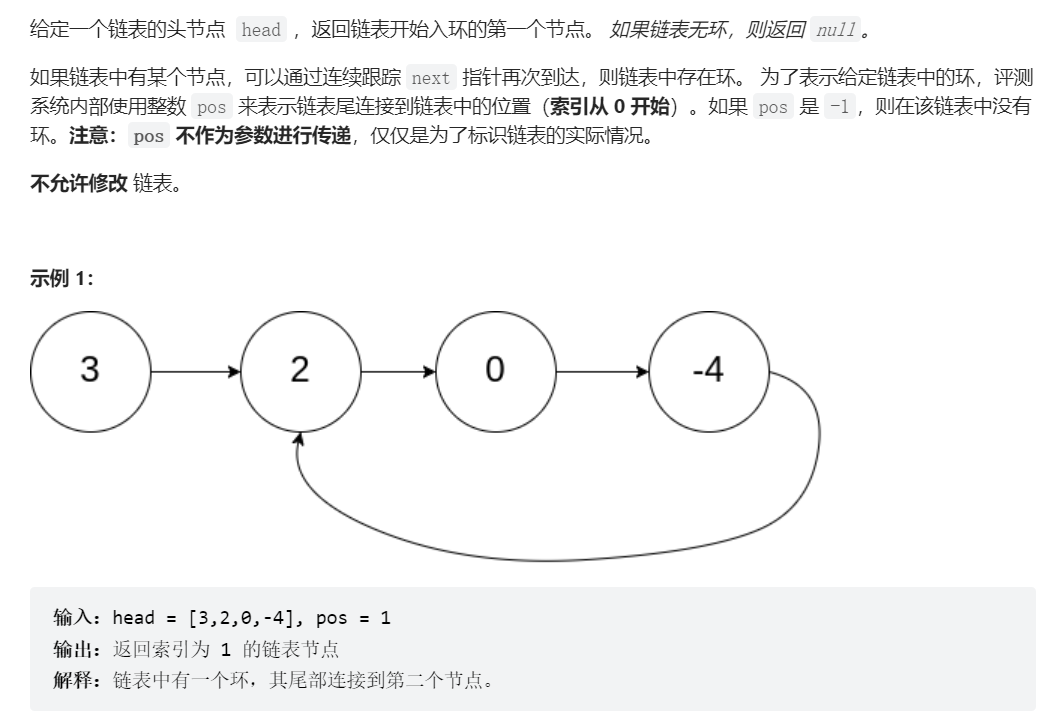
题目是这样表述的：

此题可以说是上一题的升级版，难度也有所增加。和上一题一样，我对此题也束手无策，只好从结果出发，总结总结此题。

首先最外层的肯定是先判断给的链表是否含环，这和上一题是一模一样的，难点就在于怎么找到环的入口，那就是最后一个结点的$next$所指向的节点。针对此题，有一个结论：

当$slow$进环以后，$fast$第一次与$slow$相遇时的节点到入口的距离等于链表第一个节点到环入口的距离。

简言之，就是：记$slow$与$fast$第一次相遇时的节点为$meet$，第一个节点为$head$，他们同时开始$next$，那最终一定会在环入口处相遇。

下面我们来推导证明这一结论：

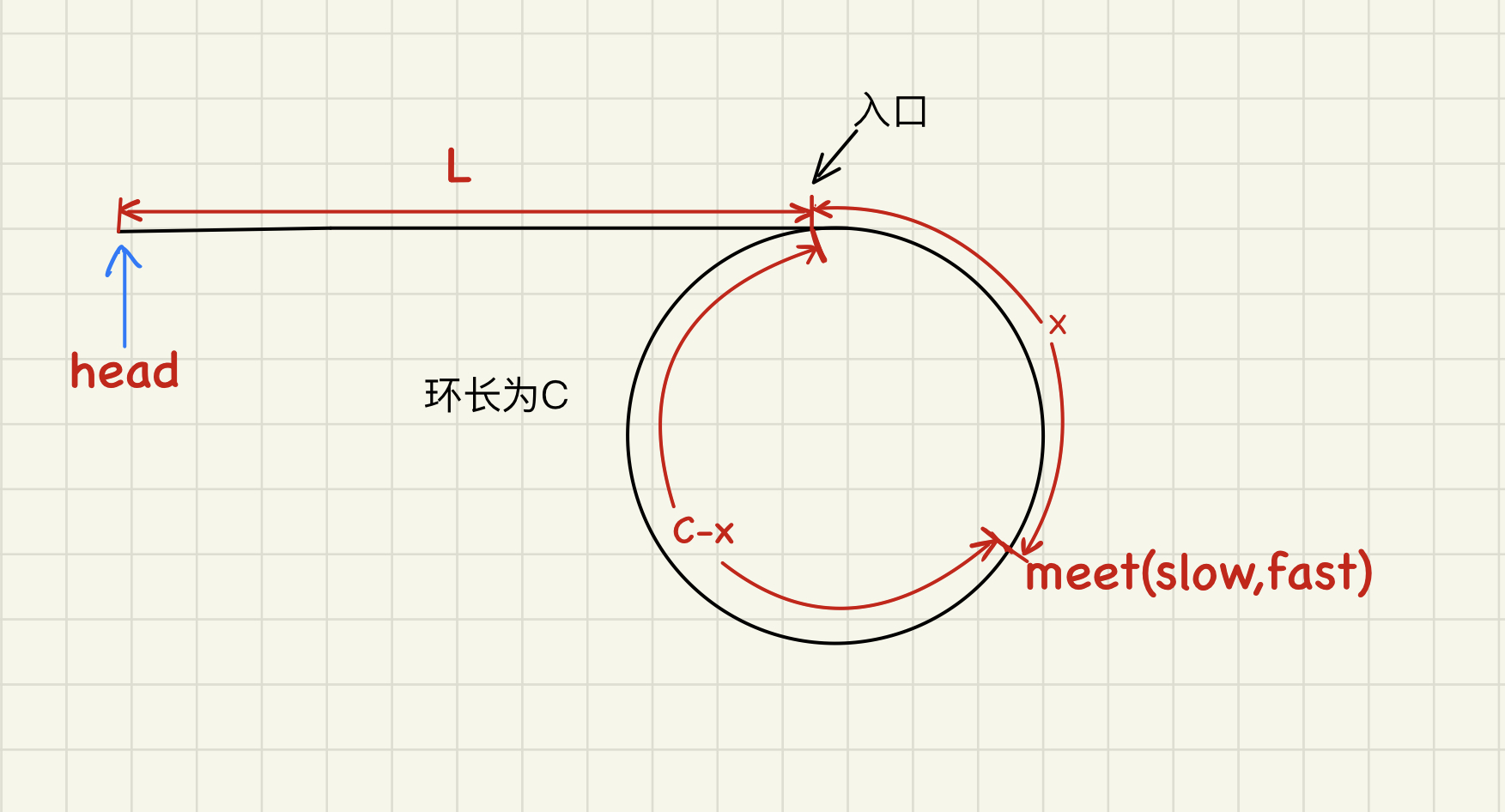
​ 示意图

通过上面的分析，很容易就可以写出代码。此题的难点就在于发现这个结论，感觉回到了一个数学问题上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *fast = head;
    struct ListNode *slow = head;
    while(fast != NULL && fast->next != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(fast == slow)
        {
            //相遇
            struct ListNode *meet = fast;
            struct ListNode *cur = head;
            while(cur != meet)
            {
                cur = cur->next;
                meet = meet->next;
            }
            return cur;
        }
    }
    return NULL;
}

喔…终于写完了-.-

-----------------------------------------------end------------------------------------------------